Cos’è Un Monomio? Una Breve Introduzione E Spiegazione

I Monomi e di conseguenza i Polinomi sono la punta dell’iceberg del calcolo letterale in matematica che viene affrontato solitamente nel programma di matematica di prima superiore.

Prima di tutto, capiamo il significato di queste parole, infatti Polinomio e Mononio deriva dal greco ”polys” molti o ”mono” uno e “nomen” termini.

Un monomio è un’espressione matematica che consiste nella moltiplicazione, bla bla bla (la riprendiamo più tardi…. 😉) Bene, passiamo alla pratica per comprendere meglio la definizione (cioè facciamo al contrario di come sempre si è fatto 😁 )

Tabella dei Contenuti

Monomi e Polinomi nella vita reale
Verifica delle competenze
Definizione di un Monomio
Esempi sui monomi
Operazioni tra Monomi
1. Somma e Sottrazione
2. Prodotto (moltiplicazione) o Divisione tra Polinomi
Definizione di un Polinomio
Domande & Risposte

Monomi e Polinomi nella vita reale

Usiamo tutti i giorni questi strumenti matematici, senza rendercene conto. Il monomio fondamentalmente è composto da una parte numerica ed una letterale:

5xyz^2 = \overbrace{5}^{parte\,numerica} \underbrace{xyz^2}_{parte\,letterale}

Bene, vi faccio due domande:

se avete 2 mele ve ne regalano altre due, quante mele avete? Beh 4 mele
se avessimo 5 mele e ne mangiassimo due, allora ne avresti 3 di mele.

é incredibile, perchè avete usato i monomi, infatti c’è una parte numerica e una parte letterale:

I monomi

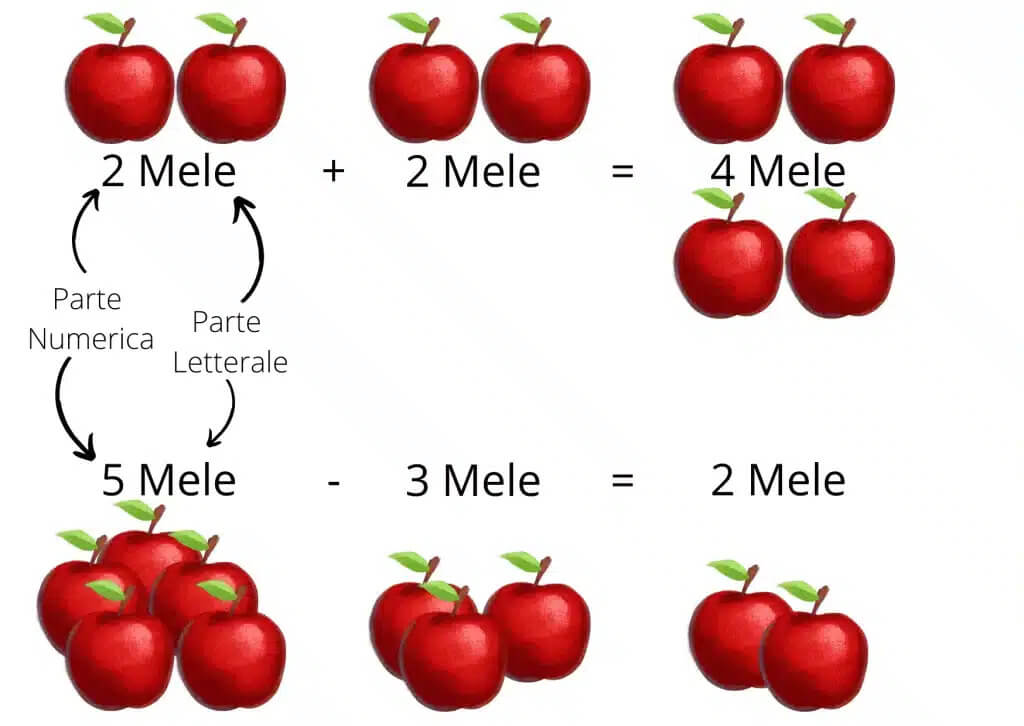
Senza saperlo avete sfruttato la regola fondamentale dei monomi:

Due monomi possono sommarsi o sottrarsi se sono simili, ovvero se hanno la stessa parte letterale.
Regola fondamentale dei monomi simili

Vediamo cosa vuol dire:

Abbiamo sommato 2 mele con 2 mele, ed abbiamo ottenuto 4 mele, ma se tu avessi 2 mele e 2 pere? Non puoi ne sommarle ne sottrarle quindi rimarrebbero così:

I monomi

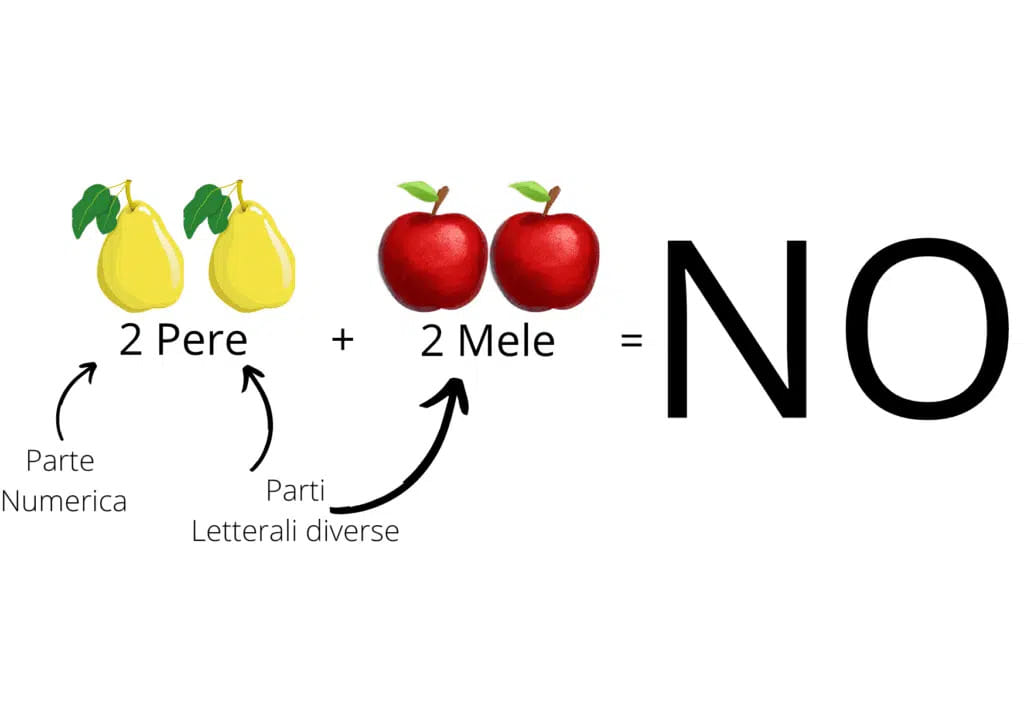
Verifica delle competenze

5xyz^2 ,\,3xyz^2

Sono monomi simili?
Si possono sommare o sottrarre tra di loro? Se si, calcola il risultato

Definizione di un Monomio

Un monomio è un’espressione matematica che consiste in un prodotto di fattori qualsiasi, siano essi numerici o letterali. I termini letterali possono essere espressi sotto forma di potenze con un numero naturale come esponente. Facciamo un esempio e commentiamolo:

2x^3

Dalla definizione di monomio vediamo i suoi termini:

Coefficiente numerico o Parte Numerica
$2$
$2$
Parte Letterale
$x^3$
$x^3$
Nella parte Letterale possono esserci solamente moltiplicazioni

Monomio Classico/Standard:

2x^3yz^2

è un monomio con parte numerica o coefficiente 2 e parte letterale

x^3yz^2

Monomio senza parte numerica:

-a^2bc =(-1)a^2bc

Se davanti al monomio non troviamo la parte numerica, è implicito che il coefficiente numerico sia 1 con il segno posto davanti al monomio in questo caso −1

Monomio con frazione nella parte numerica:

\frac{1}{2}a^2bc

è un monomio che ha parte numerica con frazione

Somma e Sottrazione

Due o più monomi per essere sommati o sottratti (differenza) devono essere simili come abbiamo visto sopra:

Somma:

a+3a+7a =(1+3+7) \cdot a = 11 a

Sottrazione:

5a-2a-a =(5-2-1) \cdot a = 2 a

Nella somma e nella sottrazione di monomi simili la parte letterale rimane sempre la stessa!

Prodotto (moltiplicazione) o Divisione tra Polinomi

Due o più monomi moltiplicati o divisi non devono essere necessariamente simili:

Moltiplicazione fra monomi simili:

2a\cdot3a =(2\cdot3) \cdot (a \cdot a )= 6a^2

Moltiplicazione fra monomi diversi (non simili):

4a\cdot3a^2 =(4\cdot3) \cdot (x \cdot y^2 )= 12xy^2

In generale si moltiplica la parte numerica del primo con quella del secondo monomio e si fa lo stesso per la parte letterale.

Divisione fra monomi simili:

\frac{3a^2}{2a} =\frac{3}{2} \cdot \frac{a^2}{a}= \frac{3}{2} \cdot a

Attenzione! Se nella moltiplicazione o divisione il monomio risultante avesse la parte letterale con un esponente negativo o comunque nella parte letterale ci fosse una frazione, esso non è più considerabile un monomio!

Moltiplicazione tra monomi simili con esponente negativo:

5x \cdot 6x^{-2} = (5\cdot 6) \cdot (x \cdot x^{-2}) =30 x^{-1} = \frac{30}{x}

Moltiplicazione tra monomi diversi (non simili) con esponente negativo:

5x \cdot 6y^{-2} = (5\cdot 6) \cdot (x \cdot y^{-2}) =30 xy^{-2} = \frac{30x}{y^2}

Divisione tra monomi diversi (non simili):

\frac{3a^2}{6x} =\frac{3}{6} \cdot \frac{a^2}{x}= \frac{1}{2} \cdot \frac{a^2}{x}

Definizione di un Polinomio

Un polinomio è semplicemente la somma o la sottrazione tra due o più monomi diversi (cioè che non hanno la stessa parte letterale):

Esempio 1:

2a + 3b

Esempio 2:

2x + 3y + 4z

Domande & Risposte

Monomio elevato a potenza

Monomio elevato alla zero?
$(2x^2y)^0 = 2^0(x^2)^0y^0 = 1$
$(2x^2y)^0 = 2^0(x^2)^0y^0 = 1$
Monomio elevato alla prima?
$(2x^2y)^1 = 2^1(x^2)^1y^1 = 2x^2y$
$(2x^2y)^1 = 2^1(x^2)^1y^1 = 2x^2y$
Monomio elevato alla seconda?
$(2x^2y)^2 = 2^2(x^2)^2y^2 = 4x^4y^2$
$(2x^2y)^2 = 2^2(x^2)^2y^2 = 4x^4y^2$
Monomio elevato alla terza?
$(2x^2y)^3 = 2^3(x^2)^3y^3 = 8x^6y^3$
$(2x^2y)^3 = 2^3(x^2)^3y^3 = 8x^6y^3$
Monomio elevato alla quarta?
$(2x^2y)^4 = 2^4(x^2)^4y^4 = 16x^8y^4$
$(2x^2y)^4 = 2^4(x^2)^4y^4 = 16x^8y^4$

Monomio, binomio e trinomio cosa sono?

Monomio: un solo termine

3xy^2

Binomio (Polinomio con due termini): somma o sottrazione di due monomi non simili (ovvero diversa parte letterale)
$3xy^2 + 4z^2$
$3xy^2 + 4z^2$
Trinomio (Polinomio con tre termini): somma o sottrazione di tre monomi non simili (ovvero diversa parte letterale)
$3xy^2 + 4z^2 + 7a$
$3xy^2 + 4z^2 + 7a$

Monomio e grado di un monomio?

Monomio di grado 0: si riferisce ad una particolare lettera mancante nella parte letterale del monomio, per esempio:
$3x^0 =3 \cdot 1 = 3$
$3x^0 =3 \cdot 1 = 3$
Monomio di grado 0: si riferisce ad una particolare lettera mancante nella parte letterale del monomio, per esempio:
$3x^0 =3 \cdot 1 = 3$
$3x^0 =3 \cdot 1 = 3$
Grado di un monomio:
- Grado di un monomio rispetto ad una lettera:
  $3a^2b^3$
  $3a^2b^3$
  Il monomio è di grado 2 rispetto ad a invece è di grado 3 rispetto b
- Grado di un monomio complessivo è la somma dei gradi delle singole lettere:
  $3+2=5$
  $3+2=5$

Monomio Nullo?

Un monomio nullo ha come parte numerica o coefficiente numerico 0.
Esempio:
$0\cdot x=0$
$0\cdot x=0$
Il monomio nullo può essere ottenuto moltiplicando qualsiasi monomio per 0. Esempio:
$0\cdot 3xy=0$
$0\cdot 3xy=0$

Monomio Opposto?

Un monomio opposto ad un altro monomio, è un monomio con stessa parte letterale ma con parte numerica opposta in segno.
Esempio:
$3xy \quad e \quad -3xy \quad | \quad \frac{3}{2}y^2 z \quad e \quad \frac{3}{2}y^2 z$
$3xy \quad e \quad -3xy \quad | \quad \frac{3}{2}y^2 z \quad e \quad \frac{3}{2}y^2 z$

Monomio Negativo?

Un monomio negativo è un monomio con parte numerica di segno negativo. Esempio:
$3xy \quad e \quad -3xy \quad | \quad \frac{3}{2}y^2 z \quad e \quad \frac{3}{2}y^2 z$
$3xy \quad e \quad -3xy \quad | \quad \frac{3}{2}y^2 z \quad e \quad \frac{3}{2}y^2 z$
Se elevo un monomio negativo per un esponente pari n=2,4,6,… otterrò sempre un monomio con parte numerica di segno positivo. Esempio:
$(-3x^2)^2 = 9x^4$
$(-3x^2)^2 = 9x^4$

Monomio simile con coefficiente reciproco?

Due monomi sono simili quando la loro parte letterale è uguale. Quindi il coefficiente reciproco si riferisce alla parte numerica. Cos’è il reciproco di un numero? É un numero che moltiplicato per il suo reciproco da come risultato 1.
Esempio:
$2 \cdot \frac{1}{2} = 1$
$2 \cdot \frac{1}{2} = 1$