
Come Eseguire Calcoli Rapidi : Suggerimenti E Trucchi Per Il Tolc

Utilizzando tecniche e pratiche semplici, chiunque può imparare a eseguire calcoli complessi con facilità e velocità.
Abbiamo visto nel precedente articolo 6 Cose da fare durante il test di Medicina. All’interno dell’articolo e del video correlato parlavo di alcune cose che ti permettono di risparmiare tempo. Infatti saper calcolare in maniera veloce e bene ti permette di risparmiare un sacco di tempo che come sai è preziosissimo durante le prove dei bandi di Concorso, i TOLC e il Test di Medicina.
Poiché il MIUR da Bando non permette l’uso della calcolatrice è bene che impari qualche tecnica che ti permetta di diventare un calcolatore umano o quasi.
Tabella dei Contenuti
Quadrato del Binomio Esempio 1 quadrato del binomio Esempio 2 quadrato del binomio Divisione Esempio Divisione Radici Quadrate alla velocità della luce! Esempio 1 Esempio 2 Logaritmi Teorema del Prodotto Teorema del Rapporto Teorema del Rapporto Esempio 1 Conclusione
Semplifica i calcoli complessi scomponendoli
Se avete difficoltà con calcoli complessi, un approccio è quello di suddividerli in passaggi più piccoli e gestibili. Ad esempio, se dovete calcolare l’area di una forma irregolare con più lati e angoli, suddividetela in forme più piccole che potete calcolare facilmente e poi sommatele alla fine. Questo approccio può essere applicato anche alle equazioni algebriche: scomponetele in parti più piccole, più facili da risolvere e da combinare alla fine. Scomponendo calcoli complessi in calcoli più semplici, è possibile migliorare la comprensione del problema e renderlo meno complesso da affrontare. Vediamo una serie di esempi con tutte le operazioni possibili!
Addizioni e Sottrazioni
Il metodo classico che ti hanno insegnato a scuola non è molto agile, anzi è molto macchinoso e poco naturale: la somma o sottrazione in colonna. Vediamo un esempio:
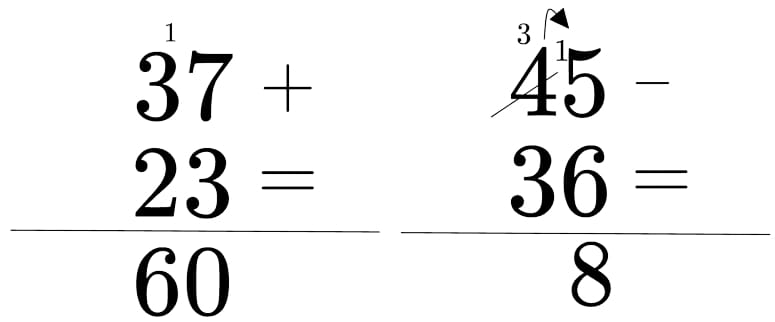
Adesso, poi veder in maniera più semplice ed intuitiva la somma di due numeri come tante piccole sotto operazioni, infatti puoi scomporre i numeri, in maniera tale da semplificarti le operazioni. Per la stessa operazione puoi scomporre i vari numeri in maniera diversa “personalizzandoli”, ma ti spiego meglio negli esempi.
Utilizza queste tecniche di matematica mentale:
Operazioni di Somma
Metodo 1:
Posso pensare il numero 37 come la somma tra 35+2. Adesso la somma mi risulterà più semplice.
Metodo 2:
Puoi pensare il numero 65 e 37 rispettivamente come la somma tra 60+5 e 35+2. Adesso la somma mi risulterà più semplice da calcolare.
Metodo 3:
Puoi pensare il numero 37 come la somma tra 30+7 ed eseguire le varie operazioni di somma in maniera più facile e veloce.
Insomma, credo che tu abbia capito il concetto, in linea di massima ti conviene “smontare” i numeri per poter fare operazioni più piccole, quindi più facili e più frammentate! Per farti capire meglio, voglio fare ancora qualche esempio:
- Metodo 4: Metodo di Somma con “Sottrazione”
Puoi pensare il numero 19 come la sottrazione tra 20-1 ed eseguire le varie operazioni di somma in maniera più facile e veloce.
Infatti, se hai un numero, che ha la prima cifra a destra uguale a zero, ti dovrai preoccupare solo delle decine e l’operazione risulterà molto più semplice.
Operazioni di Sottrazione
La sottrazione deve essere fatta allo stesso modo della somma ovvero “giocando” con i numeri, in maniera tale da semplificarmi le operazioni al massimo:
Metodo 1:
Come vedi, puoi far combaciare le due cifre delle unita, in maniera tale da sapere che la loro sottrazione è perfetta e quindi il risultato sarà pari a 0.
Metodo 2:
Stai facendo come sopra ma stai agendo sul secondo numero.
Metodo 3:
Questo è più simile a quello che avevamo fatto nella somma, ma è comunque valido e se non ti va di ricordarti troppe regole, io sono pigro e approvo! 😁
Moltiplicazione e Divisione
Il metodo classico che ti hanno insegnato a scuola non è molto agile, anzi è molto macchinoso e poco funzionale. Per fare le moltiplicazioni e le divisioni sei già a metà strada, poichè il metodo che userai comprende anche quello che hai imparato per la somma o sottrazione che hai visto sopra. Vediamo un esempio:
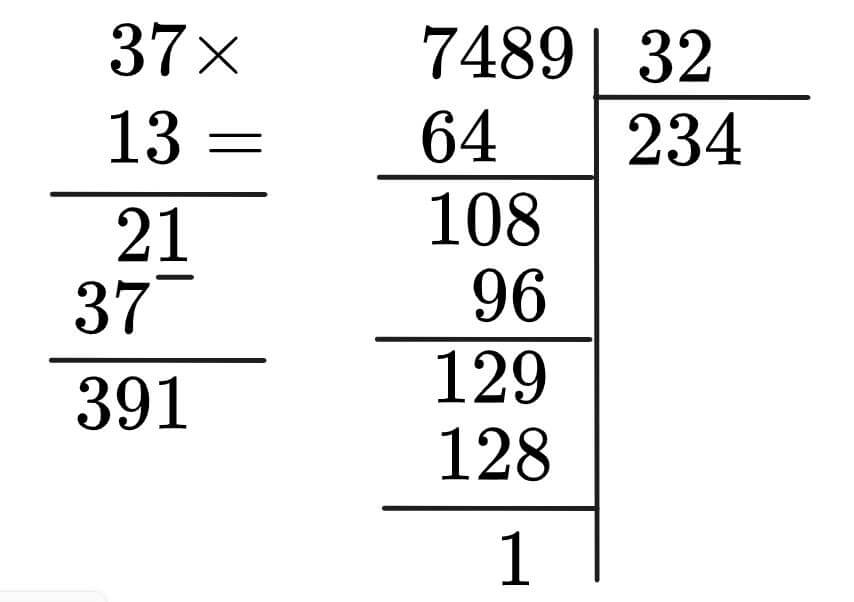
Prima di tutto dovresti conoscere almeno le tabelline fino a quella del 10. Ti ricordo che alcune tabelline hanno dei trucchetti per essere ricordate, ad esempio quella del 9. Se guardate i numeri sulla colonna di destra finiscono come se fosse un count-down dal 9 allo 0.
| Tabellina del | Nove |
|---|---|
| 9x1 | 9 |
| 9x2 | 18 |
| 9x3 | 27 |
| 9x4 | 36 |
| 9x5 | 45 |
| 9x6 | 54 |
| 9x7 | 63 |
| 9x8 | 72 |
| 9x9 | 81 |
| 9x10 | 90 |
Bene passiamo ai trucchetti.
Operazioni di Moltiplicazione
Per fare le moltiplicazioni al meglio, devi conoscere due proprietà facili di questa operazione: la proprietà commutativa e quella distributiva.
- Proprietà Commutativa: Scambiando l’ordine dei numeri che sto moltiplicando il risultato non cambia.
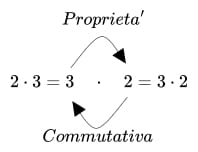
- Proprietà Distributiva: Se un numero è all’esterno di una parentesi e la moltiplica, il numero esterno andrà moltiplicato per tutti i numeri all’interno della parentesi!
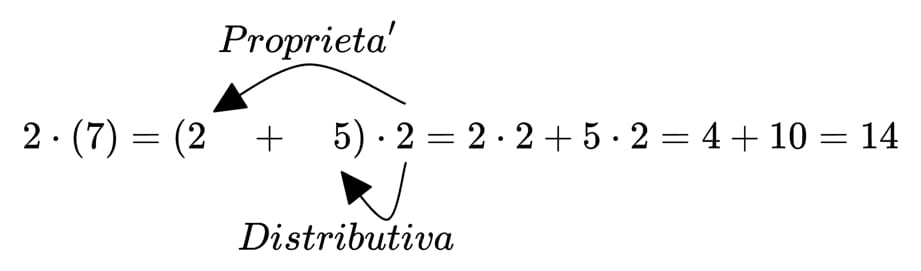
Ora che conosci queste due proprietà (eh si, puoi scordarti il nome ma non il loro funzionamento) capiamole meglio con degli esempi.
Moltiplicazioni ad una cifra
Metodo dell scomposizione
Esempio 1:
Possiamo scomporre il 20 come 10 che moltiplica 2, quindi usare la proprietà Commutativa per moltiplicare il 7 ed il 2 tra loro ed infine moltiplicate tutto per 10, che sappiamo basta scrivere uno zero dopo il numero risultante quindi 14 e poi 0, 140!
Esempio 2:
Puoi scomporre il 37 come la somma tra 30 e 7, applicare la proprietà Distributiva, moltiplicando il 4 che è fuori parentesi con 30 e 7 che sono all’interno. Ora puoi vedere il 30 come 10 che moltiplica 3, quindi usare la proprietà Commutativa per moltiplicare il 3 ed il 4 tra loro ed infine moltiplicate tutto per 10, ottenendo 120.
Sei quasi a metà dell’opera, tieni duro.
Adesso basterà che fai 120+7⋅4, ovvero 120+28 che se vuoi puoi scomporre ulteriormente come si è fatto prima per le somme:
Metodo dell’arrotondamento:
Esempio 1:
Anche qua, il metodo è sempre lo stesso, solo che questa volta dovrai vedere 39 come 40 - 1 ed poi usare la proprietà distributiva ed il gioco è fatto.
Moltiplicazioni ad due o più cifre
Metodo della scomposizione
Il metodo è sempre lo stesso, lo avrai capito e quindi ti faccio un esempio:
Oppure te ne insegno un altro un pò più magico (in pratica sarebbe una moltiplicazione come ti hanno insegnato in colonna ma in riga, ti spiego meglio dopo)
Metodo Magico: Moltiplicazione in riga
Questo metodo lo conosci già, ma ha una forma diversa: hai sentito parlare delle moltiplicazioni in colonna? Ebbene questa è come la moltiplicazione in colonna ma su una riga. Infatti, devi fare gli stessi passaggi che faresti in colonna.
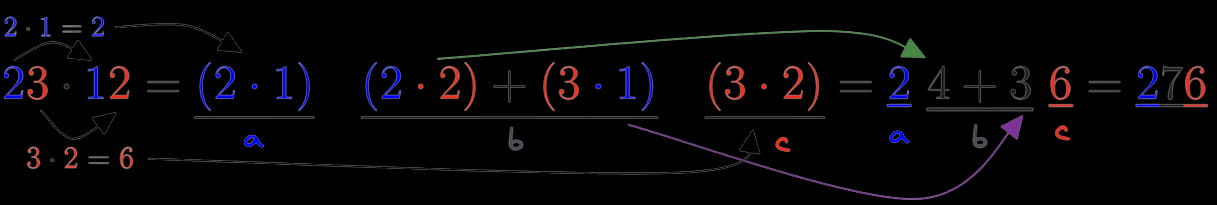
Passaggio 1: Moltiplichiamo le due in blu (quelle delle decine) fra di loro e riportiamo il loro valore nel posto a
Passaggio 2: al posto b invece riportiamo la moltiplicazione dei numeri estremi: le decine, ovvero il numero 2 del numero 23 e le unità del numero 12 ovvero il 2. Il precedente risultato dobbiamo sommarlo con il prodotto fra le unità del numero 23 ovvero il 3 e il numero 1 delle decine del 12. Una volta fatto sommiamo tutto mettendo il valore nel posto b
Passaggio 3: nel posto c invece dobbiamo mettere il prodotto tra i numeri 3 e 2 che sono rispettivamente le unità dei numeri 23 e 12
Moltiplicazioni e Potenze
Quadrato del Binomio
Il quadrato del binomio viene insegnato con i polinomi che abbiamo visto in un articolo precedente. Ti faccio un piccolo recap: il quadrato del binomio è questa operazione qua:
Questa formula puoi ricordarla o ricorrere al “metodo pigro” (il mio preferito😎) ovvero:
Adesso usando la proprietà Distributiva (spiegata sopra) puoi fare le varie operazioni, moltiplichi il primo termine etc
Esempio 1 quadrato del binomio
Il quadrato del binomio può essere usato per calcolare velocemente il quadrato di qualsiasi numero:
Esempio 2 quadrato del binomio
Se stai usando la formula del quadrato del binomio per il calcolo delle potenze. Ti consiglio di impararti le potenze più comuni in maniera tale calcolare la maggior parte delle potenze che troverai nel test.
| n | n2 |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| 16 | 256 |
| 17 | 289 |
| 18 | 324 |
| 19 | 361 |
| 20 | 400 |
Infatti a parità di domande e punteggio fatto, scalerà più in alto la graduatoria, colui che ha fatto più punti nelle domande di chimica e biologia.
Quindi concentrati sulle materie che contano!
Divisione
Per quanto riguarda la divisione, ti sconsiglio categoricamente di usare la Divisione in Colonna ma di usarla solo se strettamente necessario, per esempio se hai bisogno di scoprire precisamente le cifre dopo la virgola… Senno le frazioni sono migliori delle divisioni poiché ti permettono di usare qualche tecnica che abbiamo già visto e combinarle tutte assieme
Esempio Divisione
Radici Quadrate alla velocità della luce! Questa tecnica è fenomenale. Ti permetterà di calcolare le radici quadrate ad una velocità impressionante. Non devi nemmeno avere tutta questa conoscenza delle potenze. Questa è la potenza di questo “trucchetto matematico”:
Esempio 1
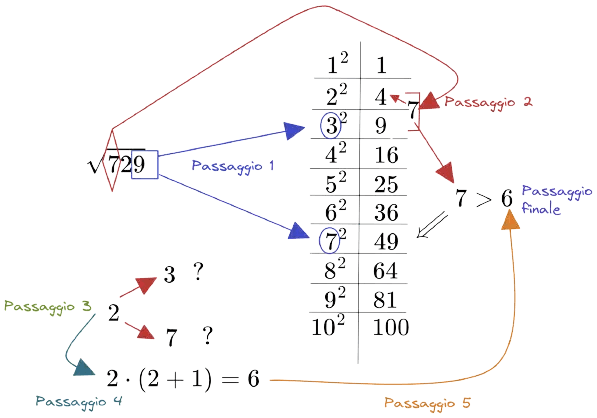
- Passaggio 1: il numero 729 finisce per 99. Nella tabella di fianco solo due numeri elevati al quadrato danno come risultato un numero che finisce per 99. Quindi so che il risultato della mia radice quadrata finira per uno di questi due numeri o 33 o 77.
- Passaggio 2: il numero sotto radice inizia con il numero 77. Questo numero, seguendo la tabella di fianco, sta tra il 4 e il 9 ovvero tra 22 e 32. Dovrai scegliere il numero minore ovvero il risultato che deriva dalla radice inizia per 22
- Passaggio 3: ora sai che il numero risultante inizia per 22 ma devi scegliere il numero con il quale finisce. Quindi potrebbe essere o 23 o 27.
- Passaggio 4: per scegliere devi moltiplicare il numero con cui inizia il risultato ovvero 22 per il suo successivo. Otterrai 2⋅3=62⋅3=6.
- Passaggio 5: Devi confrontare il numero 6 con il numero 7.
- Passaggio Finale: Il risultato del passaggio 4 è minore di 77. Per questo motivo dovrai scegliere il numero maggiore tra 32 e 72.
Esempio 2
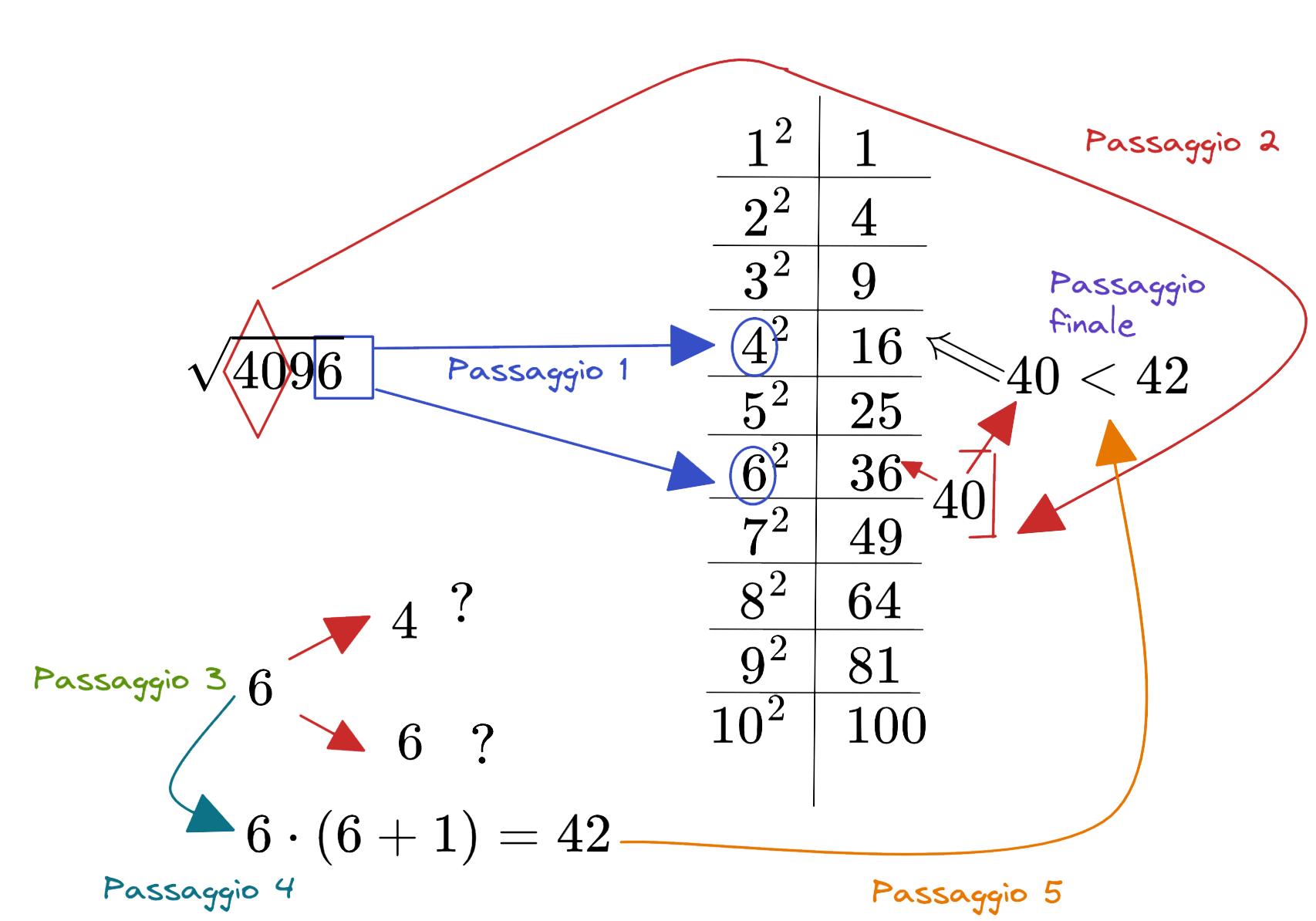
Passaggio 1: il numero 4096 finisce per 6. Nella tabella di fianco solo due numeri elevati al quadrato danno come risultato un numero che finisce per 6. Quindi so che il risultato della mia radice quadrata finira per uno di questi due numeri o 4 o 6.
Passaggio 2: il numero sotto radice, eliminate le prime due cifre finali, il numero inizia con 40. Questo numero, seguendo la tabella di fianco, sta tra il 36 e il 49 ovvero tra 62 e 72. Dovrai scegliere il numero minore ovvero il risultato che deriva dalla radice inizia per 6
Passaggio 3: ora sai che il numero risultante inizia per 66 ma devi scegliere ancora il numero con il quale finisce. Quindi potrebbe essere o 64 o 66.
Passaggio 4: per scegliere devi moltiplicare il numero con cui inizia il risultato ovvero 66 per il suo successivo. Otterrai 6⋅7=42.
Passaggio 5: Devi confrontare il numero 42 con il numero 40 (le cifre con cui inizia il numero sotto la radice).
Passaggio Finale: Il risultato del passaggio 4 è maggiore di 40. Per questo motivo dovrai scegliere il numero minore tra 42 e 62.
Logaritmi
Per i logaritmi dobbiamo tenere a mente le loro proprietà, per questo le scriveremo qua sotto, una volta che vi sono chiare potrete usare questo metodo molto facile:
Teorema del Prodotto
Teorema del Rapporto
Teorema del Esponente
Esempio 1
Il logaritmo vale circa
Conclusione
In questo articolo, ti ho elencato i trucchi di calcolo mentale più utili per risparmiare tempo, non solo nella vita ma ai tolc e al tolc di medicina Visto che a molti test non è permesso l’uso della calcolatrice. Questi consigli, sono trasversali, ovvero posso essere applicati a qualsiasi test da affrontare.
Il tolc di medicina è una sfida importante. Purtroppo, nelle scuole non vengono fornite informazioni sul come prepararsi per affrontare un test di medicina e su come comportarsi durante l’esame. Per questo motivo, è necessario adottare due strategie fondamentali per prepararsi al meglio. Queste strategie ti permetteranno di superare con successo l’esame di medicina e di avere una buona preparazione per affrontare questo difficile ostacolo. Ti lascio i link agli articoli e ai video qua sotto:
- 6 Consigli Su Come Prepararsi Al Test Di Medicina 💊 Da Soli
- Test Medicina: Trucchi Per Ottimizzare Il Tempo Durante Il Tolc 💊
Spero che i miei consigli, ti saranno utili in preparazione del test di ammissioni a Medicina e Chirurgia.
Vi lascio qua sotto il video correlato all’articolo!